Chapter 1: Fundamental

1.4 Finding Hamiltonian Path

In previous Section, we learned some of the path operators and path conditions. With a combination of path operators and compound path conditions, we are able to solve many interesting problems from graph theory. For example, Hamiltonian path problem from Introduction . In this Section, we will show you how to write a Cyclone specification to solve this problem.

The graph from Chapter 0 is shown below:

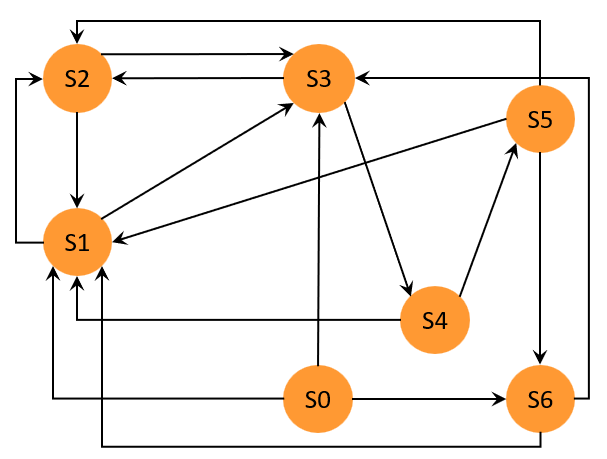
Remember the condition for finding a Hamiltonian path is that:

   covers all the nodes of a graph exactly once

Since the condition says that first we need to cover all the nodes, we know we have a total of 7 nodes ( S0 - S6 ) in our graph. Therefore, a valid Hamiltonian path for this graph must have a length of 6 . The length of a path is defined by the number of edges.

Next, we need to cover each of node exactly once. We can easily use ^{i..j} path operator to construct a path condition for each node. Finally, we do not know which node this path will reach, but what we know is it eventually will reach any of these 7 nodes (except for our starting node). So we can specify these nodes in our reach statement.

Say we define node S0 as a starting point. Hence, we now can define our goal of finding Hamiltonian path for the graph above as follows:

   check for 6 condition (

       S0^{1} && S1^{1} &&

       S2^{1} && S3^{1} &&

       S4^{1} && S5^{1} &&

       S6^{1} )

 reach (S0,S1,S2,S3,S4,S5,S6)

The full specification for this problem is shown below:

  graph HamiltonianPathExample {

       // define starting node S0.

      abstract start node  S0 {}

      abstract node  S1 {}

      abstract node  S2 {}

      abstract node  S3 {}

      abstract node  S4 {}

      abstract node  S5 {}

      abstract node  S6 {}

      edge  t1 { S0 -> S1 }

      edge  t2 { S0 -> S3 }

      edge  t3 { S0 -> S6 }

      edge  t4 { S1 -> S2 }

      edge  t5 { S1 -> S3 }

      edge  t6 { S2 -> S3 }

      edge  t7 { S2 -> S1 }

      edge  t8 { S3 -> S2 }

      edge  t9 { S3 -> S4 }

      edge  t10 { S4 -> S5 }

      edge  t11 { S4 -> S1 }

      edge  t12 { S5 -> S1 }

      edge  t13 { S5 -> S1 }

      edge  t14 { S5 -> S6 }

      edge  t15 { S6 -> S1 }

      edge  t16 { S6 -> S3 }

/*

       * Goal: Find a Hamiltonian Path, starting from node S0.

*/

     goal{

       check for 6 condition (

               S0^{1} && S1^{1} &&

               S2^{1} && S3^{1} &&

               S4^{1} && S5^{1} &&

               S6^{1} )

               reach (S0,S1,S2,S3,S4,S5,S6)

Compile this specification, and Cyclone successfully finds a Hamiltonian path for this graph:

S0->S6->S3->S4->S5->S2->S1

1.4.1 Practice.

Can you use Cyclone to find all possible Hamiltonian paths in this graph?

Can you use Cyclone to find all possible Hamiltonian cycles in this graph?

A Hamiltonian cycle is a Hamiltonian path that starts and ends with the same node.

< Previous Next >