Chapter 2: Building Simple Models

In this section, you will learn how to use Cyclone to prove a zero-sum game.

2.2 Proving Zero-sum Game

A zero-sum game essentially is a scenario that has two players, where the result is an advantage for one player and a loss for the other player.

We can write a Cyclone specification to model this scenario and prove a game indeed ensuring the sum of two player's stake is zero.

Let's assume there are two players: P1 and P2. When P1 wins a game, P1's stake gets increased by 1 and P2 loses his stake by 1. When P2 wins a game, his stake also gets increased by 1 and P1 loses his stake by 1. At the start of the game, both their stake is 0.

Hence, we can build the following state machine to describe different states for the two players.

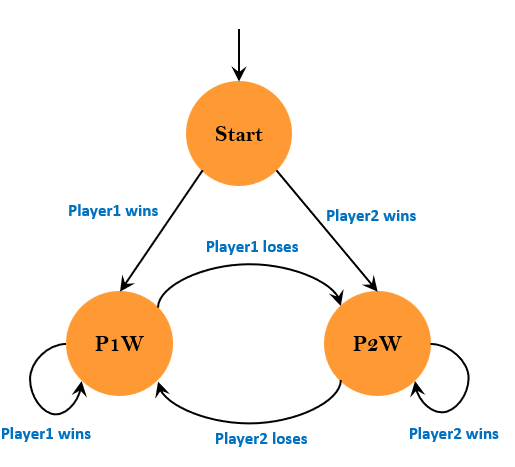
The Start state denotes our initial state and in this state both player's stake are set to 0.

      int  stake1; // player1's stake.

      int  stake2; // player2's stake.

      start normal state  Start {

        stake1 = 0;

        stake2 = 0;

From the Start state either player 1 wins (P1W) or player 2 wins (P2W). When player 1 wins, we increment his stake by 1 and decrement player2's stake by 1.

      normal state  P1W {

        stake1 = stake1 + 1;

        stake2 = stake2 - 1;

Simiarly, when player 2 wins we increment his stake by 1 and decrement player1's stake by 1.

      normal state  P2W {

        stake1 = stake1 - 1;

        stake2 = stake2 + 1;

To show this is a zero sum game, we want to prove that no matter whoever wins the stake of the winner plus the stake of the loser should always be 0. This is called an invariant. It indicates the stake from both players should always be 0 no matter which state a player is in.

In Cyclone, one could use invariant statement to specify an invariant for all states defined in a specification. Hence, we write the following invariant

  //a zero-sum invariant for two players.

  invariant  zerosum { stake1 + stake2 == 0;}

Next, we prove that if we game multiple rounds the invariant should always hold. Therefore, we write the following goal section.

     goal{

         check for 1,2,3,4,5 reach (P1W,P2W)

Here, we asks Cyclone to check 5 games. The check for statement here specifies 5 different games. For example, 1 means a game only has 1 round. When there exists an invariant in the specification, the goal section becomes to ask Cyclone to discover a counter-example. In other words, we are asking Cyclone to give us a path (counter-example) such that it will break our invariant.

In this example, it is impossible to find such a counter-example. Hence, we prove this indeed is a zero-sum game within a bound of 5 games.

< Previous Next >