Chapter 2: Building Simple Models

2.5 Model a Hybrid System

In this section, we will learn how to use Cyclone to verify a simple hybrid system. A hybrid system has both continuous and discrete dynamic behavior and it can both flow and jump. Typically, flow is described by some differential equations and jumps are modeled as a finite state machine.

To model a hybrid system, we will establish a model of physics and model of software. The physics model describes continuous dynamics and software model describes discrete dynamics.

Bouncing Ball

A classic example of a hybrid system is the bouncing ball (A system with impact). A ball is dropped from a predefined height. It then hits the ground (after a certain time), loses some energy and bounces back into the air and starts to fall again.

Its physical model can be described using the following differential equation:

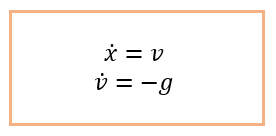
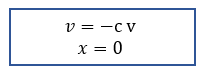
where v is our velocity (with respect to time t), x is the height, and g is the gravitational acceleration 9.81/ms². As time (t) goes by, the ball moves closer (x) to the ground and eventually hits the ground when x=0. It then dissipates its energy and starts to bounce back. This behavior is modeled using the following equation:

-c v accounts for the loss of energy due to the ball's deformation, where c ∈[0,1] is a constant.

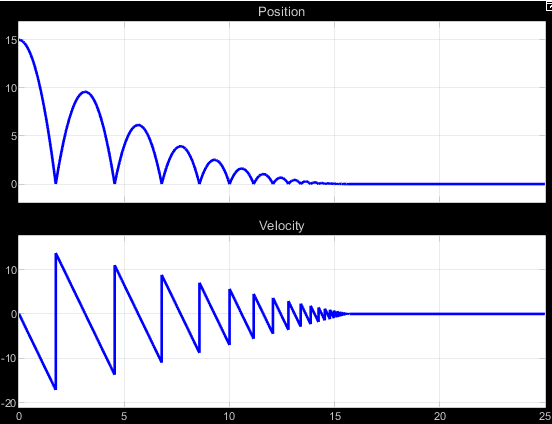
The following graphs show the position of the ball and its velocity when time passes.

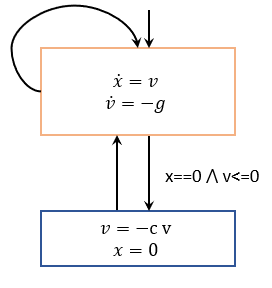
Now, We can use a finite state machine to describe discrete states of a bouncing ball. This state machine is as follows:

Further, the invariant here is no matter which state we are in our x (the height) should always stay positive (>=0). Hence, we have our Cyclone spec:

     real x where x >= 0; //height

     real v; //velocity

     real t where t > 0; //time

     const real G=9.81; //gravity acceleration

     real c where c >= 0 && c<=1; //coefficient of energy loss

     normal start state Fall{

            x = x + v * t;

            v = v - G * t;

     normal state Bounce{

              v = -c * v;

              x = 0;

     trans  t1 { Fall -> Fall }

     trans  t2 { Fall -> Bounce  where  (x<=0 && v<=0);}//guard

     trans  t3 { Bounce -> Fall }

     invariant  BouncingBallInv { x>=0; }//state invariant

Next, we can just specify our goal section to ask Cyclone to check for specific traces of a counter-example.

     goal {

          check for 2,3,4,5  reach (Fall,Bounce)

< Previous Next >